Matrix Inverse
Linear system
We have matrix $\boldsymbol{A}: m \times n$, and vectors $\boldsymbol{b}: m \times 1$ and $\boldsymbol{x}: n \times 1$ where $\boldsymbol{b}$ is given and $\boldsymbol{x}$ is unknown. We use the equation
$$ \boldsymbol{Ax} = \boldsymbol{b} $$
We’re interested in when does a solution $\boldsymbol{x}$ exist, and how do we find it.
A linear system is consistent when there exists at least one $\boldsymbol{x}$ satisfying the equation. We can see that the following statements are equivalent:
- A linear system is consistent.
- $\boldsymbol{b} \in \mathcal{C}(\boldsymbol{A})$.
- $\mathcal{C}([\boldsymbol{A}, \boldsymbol{b}]) = \mathcal{C}(\boldsymbol{A})$.
- $r([\boldsymbol{A}, \boldsymbol{b}]) = r(\boldsymbol{A})$.
If $\boldsymbol{A}$ has full row rank $m$, then $\mathcal{C}(\boldsymbol{A}) = \mathbb{R}^m$, and $\boldsymbol{Ax} = \boldsymbol{b}$ is consistent for any $\boldsymbol{b}$.
The next fact is important in statistical contexts. The linear system $\boldsymbol{A}’\boldsymbol{Ax} = \boldsymbol{A}’\boldsymbol{b}$ is consistent for any $\boldsymbol{A}$, $\boldsymbol{b}$. This is because $\boldsymbol{A}’\boldsymbol{b} \in \mathcal{C}(\boldsymbol{A}’) = \mathcal{C}(\boldsymbol{A}’\boldsymbol{A})$.
If $\boldsymbol{A}$ has full column rank, $\boldsymbol{A}’\boldsymbol{A}$ is nonsingular, and $\boldsymbol{x}$ is unique. This is an assumption in our regression analyses, which is there’s no redundancy in our predictor variables.
Matrix inverse
The inverse of a matrix only makes sense when the matrix is square. Before talking about it, we introduce two other concepts for non-square matrices.
Left and right inverses
If $\boldsymbol{A}: m \times n$, the right inverse $\boldsymbol{R}$ is the $n \times m$ matrix such that
$$ \boldsymbol{AR} = \boldsymbol{I}_m $$
The right inverse exists when $\boldsymbol{A}$ has full row rank, i.e. $r(\boldsymbol{A}) = m$ ($m \leq n$). This is because if $r(\boldsymbol{A}) = m$, then $\boldsymbol{Ax} = \boldsymbol{b}$ is consistent for any $\boldsymbol{b}$. Let
$$ \boldsymbol{b}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix}_{m \times 1}, \boldsymbol{b}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}, \cdots, \boldsymbol{b}_m = \begin{pmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix} $$
The solution for $\boldsymbol{Ab}_1 = \boldsymbol{x}$ is $\boldsymbol{x}_1$, and similarly we have $\boldsymbol{x}_2, \cdots, \boldsymbol{x}_m$. If we put $\boldsymbol{x}_1, \cdots, \boldsymbol{x}_m$ into an $n \times m$ matrix
$$ \boldsymbol{R} = [\boldsymbol{x}_1, \cdots, \boldsymbol{x}_m], $$
we have $\boldsymbol{AR} = \boldsymbol{A}[\boldsymbol{x}_1, \cdots, \boldsymbol{x}_m] = \boldsymbol{I}_m$. From the proof we can also see that $\boldsymbol{R}$ is not unique.
Similarly, the left inverse $\boldsymbol{L}: n \times m$ is the matrix that satisfies $\boldsymbol{LA} = \boldsymbol{I}_n$. $\boldsymbol{L}$ exists when $\boldsymbol{A}$ has full column rank, i.e. $r(\boldsymbol{A}) = n (m \geq n)$.
Inverse
If $\boldsymbol{A}$ is non-singular, then its right inverse and left inverse exist, and they are the same, which we call the inverse of $\boldsymbol{A}$ denoted by $\boldsymbol{A}^{-1}$. $\boldsymbol{A}^{-1}$ is unique. To prove this, note that
$$ \boldsymbol{L} = \boldsymbol{LI}_n = \boldsymbol{LAR} = \boldsymbol{I}_n \boldsymbol{R} = \boldsymbol{R} $$
Properties
If $\boldsymbol{A}$ has full column rank $n$1, and there exists $\boldsymbol{L}$ such that $\boldsymbol{LA} = \boldsymbol{I}_n$ ($n \leq m$), then
$\boldsymbol{B} = \boldsymbol{C} \Longleftrightarrow \boldsymbol{AB} = \boldsymbol{AC}$
This is because
$$ \boldsymbol{AB} = \boldsymbol{AC} \Rightarrow \boldsymbol{LAB} = \boldsymbol{LAC} \Rightarrow \boldsymbol{I}_n\boldsymbol{B} = \boldsymbol{I}_n \boldsymbol{C} $$
For any $\boldsymbol{B}$, $r(\boldsymbol{AB}) = r(\boldsymbol{B})$. Pre-multiplying a full column rank matrix does not change the rank.
For any $\boldsymbol{B}$, $\mathcal{R}(\boldsymbol{AB}) = \mathcal{R}(\boldsymbol{B})$ when $\boldsymbol{A}$ has full column rank.
If $\boldsymbol{A}$ has full column rank $n$, then $\boldsymbol{A}’\boldsymbol{A}$ is non-singular and vice versa. Similarly if $\boldsymbol{A}$ has full row rank, $\boldsymbol{AA}’$ is non-singular.
Inverse of non-singular matrix
Suppose $\boldsymbol{A}$ is an $m \times m$ non-singular matrix.
If $m = 2$, we have
$$ \boldsymbol{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}, \quad \boldsymbol{A}^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} $$
Check that $\boldsymbol{AA}^{-1} = \boldsymbol{I}_2$ to make sure.
If $\boldsymbol{A}$ is diagonal and all diagonals are non-zero,
$$ \boldsymbol{A}^{-1} = diag \left(d_1^{-1}, \cdots, d_m^{-1} \right) $$
$\boldsymbol{Ax} = \boldsymbol{b}$ has a unique solution $\boldsymbol{x} = \boldsymbol{A}^{-1}\boldsymbol{b}$.
$(k\boldsymbol{A})^{-1} = \frac{1}{k}\boldsymbol{A}^{-1}$.
$\boldsymbol{A}’$ is also non-singular, and its inverse is
$$ (\boldsymbol{A}’)^{-1} = (\boldsymbol{A}^{-1})' $$
This is because if we take the transpose of both sides of $\boldsymbol{AA}^{-1} = \boldsymbol{I}_m$, we get $(\boldsymbol{A}^{-1})’\boldsymbol{A}’ = \boldsymbol{I}_m$. Since $\boldsymbol{A}’$ is non-singular, $(\boldsymbol{A}^{-1})’$ is the inverse of $\boldsymbol{A}’$.
$\boldsymbol{A}^{-1}$ is also non-singular, i.e. $r(\boldsymbol{A}^{-1}) = m$. This is because
$$ m = r(\boldsymbol{AA}^{-1}) \leq r(\boldsymbol{A}^{-1}) \leq m $$
If $\boldsymbol{B}$ is also an $m \times m$ non-singular matrix, then $\boldsymbol{AB}$ is also non-singular, and $(\boldsymbol{AB})^{-1} = \boldsymbol{B}^{-1}\boldsymbol{A}^{-1}$. To check this claim,
$$ (\boldsymbol{AB})(\boldsymbol{B}^{-1}\boldsymbol{A}^{-1}) = \boldsymbol{AI}_m\boldsymbol{A}^{-1} = \boldsymbol{AA}^{-1} = \boldsymbol{I}_m $$
This could be generalized to the product of $k$ non-singular matrices: $(\boldsymbol{A}_1\boldsymbol{A}_2 \cdots \boldsymbol{A}_k)^{-1} = \boldsymbol{A}_k^{-1} \cdots \boldsymbol{A}_1^{-1}$. This is similar to the transpose of the product of matrices.
If $\boldsymbol{A}: m \times n$ and $r(\boldsymbol{A}) = r$; $\boldsymbol{B}: m \times m$ is non-singular, then $r(\boldsymbol{BA}) = r$. Similarly if $\boldsymbol{C}: n \times n$ is non-singular, $r(\boldsymbol{AC}) = r$. In fact, $\boldsymbol{B}$ only needs to have full column rank, and $\boldsymbol{C}$ only needs to have full row rank.
Orthonormal matrices
An orthogonal matrix, or orthonormal matrix to be more precise, is a square matrix whose columns and rows are orthonormal. One way to express this is
$$ \boldsymbol{AA}’ = \boldsymbol{A}’\boldsymbol{A} = \boldsymbol{I}_n $$
By definition, the columns have to be orthonormal because
$$ \begin{gathered} \boldsymbol{a}_i’\boldsymbol{a}_i = 1 = \|\boldsymbol{a}_i \|^2 \\ \boldsymbol{a}_i’\boldsymbol{a}_j = 0 \end{gathered} $$
Equivalently, $\boldsymbol{A}$ is orthogonal if $\boldsymbol{A}^{-1} = \boldsymbol{A}’$.
Examples
In general, any $2 \times 2$ orthogonal matrix $\boldsymbol{P}$ is
$$ \boldsymbol{P} = \begin{pmatrix} \sin\theta & -\cos\theta \\ \cos\theta & \sin\theta \end{pmatrix} $$
If we think of the matrix as an operator on a vector $\boldsymbol{u}$, the vector $\boldsymbol{v} = \boldsymbol{Pu}$ can be interpreted as a rotation of $\boldsymbol{u}$ by $\theta$ degrees. This is why $\boldsymbol{P}$ is sometimes called the rotation matrix. Note that this operation applies to higher-order matrices as well. For example, in PCA we can enforce zero-correlation by rotation.
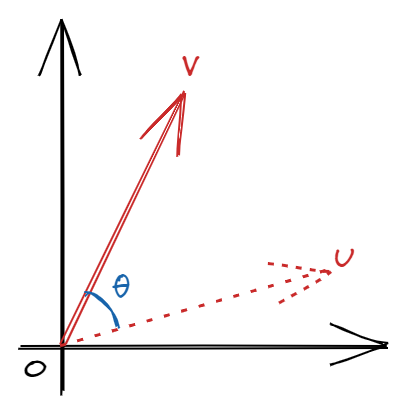
The identity matrix is also obviously orthogonal. We can also permute the columns and the resulting matrix is still orthogonal. Geometrically, this is permuting the coordinate axes.
Properties
The product of two orthogonal matrices is orthogonal.
To prove this, let $\boldsymbol{P}$ and $\boldsymbol{Q}$ be two orthogonal matrices. We then have
$$ (\boldsymbol{PQ})(\boldsymbol{PQ})’ = \boldsymbol{PQ}\boldsymbol{Q}’\boldsymbol{P}’ = \boldsymbol{PP}’ = \boldsymbol{I} $$
For any vector $\boldsymbol{x} \in \mathbb{R}^n$, $\| \boldsymbol{Px} \|^2 = \|\boldsymbol{x}\|^2$. Pre-multiplying an orthogonal matrix to a vector doesn’t change the norm of the vector because
$$ (\boldsymbol{Px})’(\boldsymbol{Px}) = \boldsymbol{x}’\boldsymbol{P}’\boldsymbol{Px} = \boldsymbol{x}’\boldsymbol{x} = \|\boldsymbol{x}\|^2 $$
For any vector $\boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n$, their inner product is not changed by pre-multiplying an orthogonal matrix
$$ (\boldsymbol{Px})’(\boldsymbol{Py}) = \boldsymbol{x}’\boldsymbol{y} $$
We can make similar arguments if $\boldsymbol{A}$ has full row rank. Just consider switching the orders. ↩︎
| Aug 31 | Vector Space | 8 min read |
| Nov 04 | Quadratic Form | 15 min read |
| Oct 26 | Determinant | 6 min read |
| Oct 23 | Projection Matrix | 4 min read |
| Oct 21 | Generalized Inverse | 4 min read |
 Yi's Knowledge Base
Yi's Knowledge Base