Projection
Now that all the basic definitions are given, we’re ready to talk about the most important part in this chapter: projection.
Projection (of a vector) onto a vector
For vectors $\boldsymbol{u}, \boldsymbol{v} \in V$, $P(\boldsymbol{u} \mid \boldsymbol{v})$ is called the projection of $\boldsymbol{u}$ onto $\boldsymbol{v}$ if:
- $P(\boldsymbol{u} \mid \boldsymbol{v})$ is proportional to $\boldsymbol{v}$, i.e. $P(\boldsymbol{u} \mid \boldsymbol{v}) = b\boldsymbol{v}$ for some $b \in \mathbb{R}$.
- $\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v})$ is orthogonal to $\boldsymbol{v}$.
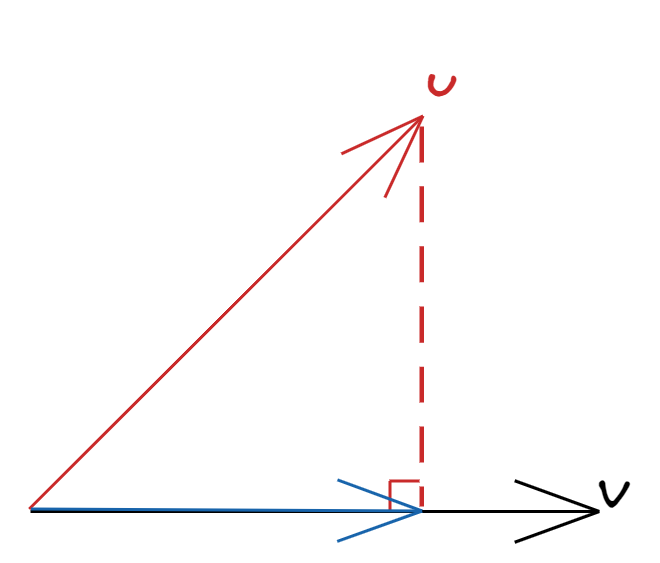
To find the projection, we just need to find the scalar $b$. By condition 2, $u\boldsymbol{u} - b\boldsymbol{v} \perp \boldsymbol{v}$, so if we take the inner product:
$$ \begin{gathered} (\boldsymbol{u} - b\boldsymbol{v})^\prime \boldsymbol{v} = \boldsymbol{u}^\prime \boldsymbol{v} - b \boldsymbol{v}^\prime \boldsymbol{v} = 0 \\ \boldsymbol{u}^\prime \boldsymbol{v} - b \|\boldsymbol{v}\|^2 = 0 \\ b = \frac{\boldsymbol{u}^\prime \boldsymbol{v}}{\|\boldsymbol{v}\|^2} \end{gathered} $$
In general,
$$ P(\boldsymbol{u} \mid \boldsymbol{v}) = \left( \frac{\boldsymbol{u}^\prime \boldsymbol{v}}{\|\boldsymbol{v}\|^2} \right) \boldsymbol{v} $$
For example, if $\boldsymbol{u} = (1, 1, 2, -1)^\prime$ and $\boldsymbol{v} = (0, 2, -2, 1)^\prime$, the projection of $\boldsymbol{u}$ onto $\boldsymbol{v}$ is
$$ \begin{aligned} P(\boldsymbol{u} \mid \boldsymbol{v}) &= \frac{2 - 4 - 1}{4 + 4 + 1} (0, 2, -2, 1)^\prime \\ &= -\frac{1}{3} (0, 2, -2, 1)^\prime = \left( 0, -\frac{2}{3}, \frac{2}{3}, -\frac{1}{3} \right)^\prime \end{aligned} $$
We can also show $\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v}) \perp \boldsymbol{v}$ by showing that:
$$ (\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v}))^\prime \boldsymbol{v} = 0 \Leftrightarrow \boldsymbol{u}^\prime \boldsymbol{v} = P(\boldsymbol{u} \mid \boldsymbol{v})^\prime \boldsymbol{v} $$
In other words, the inner product between $\boldsymbol{u}$ and $\boldsymbol{v}$ is equal to the inner product between the projection of $\boldsymbol{u}$ onto $\boldsymbol{v}$ and $\boldsymbol{v}$.
$$ \begin{aligned} P(\boldsymbol{u} \mid \boldsymbol{v}) &= \|P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 + \|\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 \\ &= \|b\boldsymbol{v}\|^2 + \|\boldsymbol{u} - b\boldsymbol{v}\|^2 \\ &= b^2\|\boldsymbol{v}\|^2 + \|\boldsymbol{u}\|^2 + b^2 \|\boldsymbol{v}\|^2 - 2b\boldsymbol{u}^\prime\boldsymbol{v} \\ &= 2\left( \frac{\boldsymbol{u}^\prime \boldsymbol{v}}{\|\boldsymbol{v}\|^2} \right)^2 \|\boldsymbol{v}\|^2 + \|\boldsymbol{u}\|^2 - 2 \frac{(\boldsymbol{u}^\prime \boldsymbol{v})^2}{\|\boldsymbol{v}\|^2} \\ &= \|\boldsymbol{u}\|^2 \end{aligned} $$
Cauchy-Schwarz inequality
By the Pythagorean theorem,
$$ \begin{aligned} \|\boldsymbol{u}\|^2 &= \|P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 + \|\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 \\ & \geq \|P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 \\ &= \|b\boldsymbol{v}\|^2 = \frac{(\boldsymbol{u}^\prime \boldsymbol{v})^2}{\|\boldsymbol{v}\|^2} \end{aligned} $$
Thus,
$$ \|\boldsymbol{u}\|^2 \geq \frac{(\boldsymbol{u}^\prime \boldsymbol{v})^2}{\|\boldsymbol{v}\|^2} \Leftrightarrow (\boldsymbol{u}^\prime \boldsymbol{v})^2 \leq \|\boldsymbol{u}\|^2 \|\boldsymbol{v}\|^2 $$
Meaning of projection
Theorem: Among all scalar multiples of $\boldsymbol{v}$, $a\boldsymbol{v}$ $a \in \mathbb{R}$, the projection of $\boldsymbol{u}$ onto $\boldsymbol{v}$ is the closest1 vector to $\boldsymbol{u}$.
To prove this, we will show
$$ \underset{a}{\text{argmin}} \|\boldsymbol{u} - a\boldsymbol{v}\|^2 = \frac{\boldsymbol{u}^\prime\boldsymbol{v}}{\|\boldsymbol{v}\|^2} $$
Here we’re minimizing the squared distance between $\boldsymbol{u}$ and $a\boldsymbol{v}$.
$$ \begin{aligned} \|\boldsymbol{u} - a\boldsymbol{v}\|^2 &= \|\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v}) + P(\boldsymbol{u} \mid \boldsymbol{v}) - a\boldsymbol{v}\|^2 \\ &= \|\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 + \|P(\boldsymbol{u} \mid \boldsymbol{v}) - a\boldsymbol{v}\|^2 + \underbrace{2(u - P(\boldsymbol{u} \mid \boldsymbol{v}))^\prime(P(\boldsymbol{u} \mid \boldsymbol{v}) - a\boldsymbol{v})}_{=0} \end{aligned} $$
Note that the first term doesn’t contain $a$, so we don’t have to consider it when minimizing w.r.t. $a$. The second term $P(\boldsymbol{u} \mid \boldsymbol{v}) - a\boldsymbol{v}$ becomes zero when $a\boldsymbol{v} = P(\boldsymbol{u} \mid \boldsymbol{v})$, attaining its minimum value. Thus,
$$ \min \|\boldsymbol{u} - a\boldsymbol{v}\|^2 = \|\boldsymbol{u} - P(\boldsymbol{u} \mid \boldsymbol{v})\|^2 \qquad \text{when } a = \frac{\boldsymbol{u}^\prime\boldsymbol{v}}{\|\boldsymbol{v}\|^2} $$
For example, for vector $\boldsymbol{y} = (y_1, \cdots, y_n)^\prime \in \mathbb{R}^n$, our goal is to find a scalar $a$ that is closet to $\boldsymbol{y}$, i.e. find $a \boldsymbol{1}_n = (a, a, \cdots, a)^\prime$ that is closest to $\boldsymbol{y}$.
$$ \begin{aligned} P(\boldsymbol{y} \mid \boldsymbol{1}_n) &= \left( \frac{\boldsymbol{y}^\prime \boldsymbol{1}_n}{1^2 + 1^2 + \cdots + 1^2} \right)\boldsymbol{1}_n \\ &= \frac{y_1 + y_2 + \cdots + y_n}{n} \boldsymbol{1}_n \\ &= \bar{y} \boldsymbol{1}_n \end{aligned} $$
Therefore $\bar{y}$ is closest to the data $(y_1, \cdots, y_n)^\prime$, or
$$ \bar{y} = \underset{a}{\text{argmin}} \sum_{i=1}^n (y_i - a)^2 = \underset{a}{\text{argmin}} \|\boldsymbol{y} - a\boldsymbol{1}_n\|^2 $$
Geometrically speaking, the sample mean deviance vector is orthogonal to the vector of sample means:
$$ \begin{pmatrix} y_1 - \bar{y} \\ y_2 - \bar{y} \\ \vdots \\ y_n - \bar{y} \end{pmatrix} \perp \begin{pmatrix} \bar{y} \\ \bar{y} \\ \vdots \\ \bar{y} \end{pmatrix} \Leftrightarrow \frac{1}{n-1}\sum_{i=1}^n (y_i - \bar{y}) \perp \bar{y} $$
This means the sample variance is uncorrelated with the sample mean. In terms of repeated sampling, if we plot the variance of each sample against the sample means, there should be no patterns.
Subspace projection
Vector $\boldsymbol{x}$ is orthogonal to a vector space $V$ if $\boldsymbol{x} \perp \boldsymbol{y}$ for all $\boldsymbol{y} \in V$. $P(\boldsymbol{u} \mid V)$ is called the projection of a vector onto a subspace if
- $P(\boldsymbol{u} \mid V) \in V$, and
- $\boldsymbol{u} - P(\boldsymbol{u} \mid V) \perp V$.
In terms of inner products, we need to have
$$ \boldsymbol{u} \cdot \boldsymbol{v} = P(\boldsymbol{u} \mid V) \cdot \boldsymbol{v} $$
Lemma: Suppose $\{\boldsymbol{u}_1, \cdots, \boldsymbol{u}_n\}$ spans $V$, then
$$ \boldsymbol{x} \perp V \Leftrightarrow \boldsymbol{x} \perp \boldsymbol{u}_j, \quad j = 1, \cdots, n $$
In other words, we only need to see the orthogonality with vectors in a spanning set.
Proving $\Rightarrow$ is trivial because it’s true by definition of orthogonality to a vector space. To prove $\Leftarrow$, for all $\boldsymbol{v} \in V$, we will show if $\boldsymbol{x} \perp \boldsymbol{u}_j$, then $\boldsymbol{x} \perp \boldsymbol{v}$.
As $\{\boldsymbol{u}_1, \cdots, \boldsymbol{u}_n\}$ is a spanning set, we can express $\boldsymbol{v}$ as a linear combination of the $\boldsymbol{u}$’s:
$$ \boldsymbol{v} = \sum_{j=1}^n \alpha_j \boldsymbol{u}_j \quad \text{for some } \alpha_j $$
The inner product between $\boldsymbol{x}$ and $\boldsymbol{v}$ is
$$ \begin{aligned} \boldsymbol{x} \cdot \boldsymbol{v} &= \boldsymbol{x} \cdot \left( \sum_{j=1}^n \alpha_j \boldsymbol{u}j \right) \\ &= \sum{j=1}^n \alpha_j (\boldsymbol{x} \cdot \boldsymbol{u}j) \\ &= \sum{j=1}^n \alpha_j \cdot 0 = 0 \end{aligned} $$
Theorem
Suppose $V$ is a subspace of $\mathbb{R}^n$, and $\{\boldsymbol{u}_1, \cdots, \boldsymbol{u}_k\}$ is an orthogonal basis for $V$. For $\boldsymbol{u} \in \mathbb{R}^n$, the projection of $\boldsymbol{u}$ onto subspace $V$ is
$$ P(\boldsymbol{u} \mid V) = \sum_{i=1}^k P(\boldsymbol{u} \mid \boldsymbol{u}i) = \sum{i=1}^k \frac{\boldsymbol{u}^\prime \boldsymbol{u}_i}{\|\boldsymbol{u}_i\|^2} \boldsymbol{u}_i $$
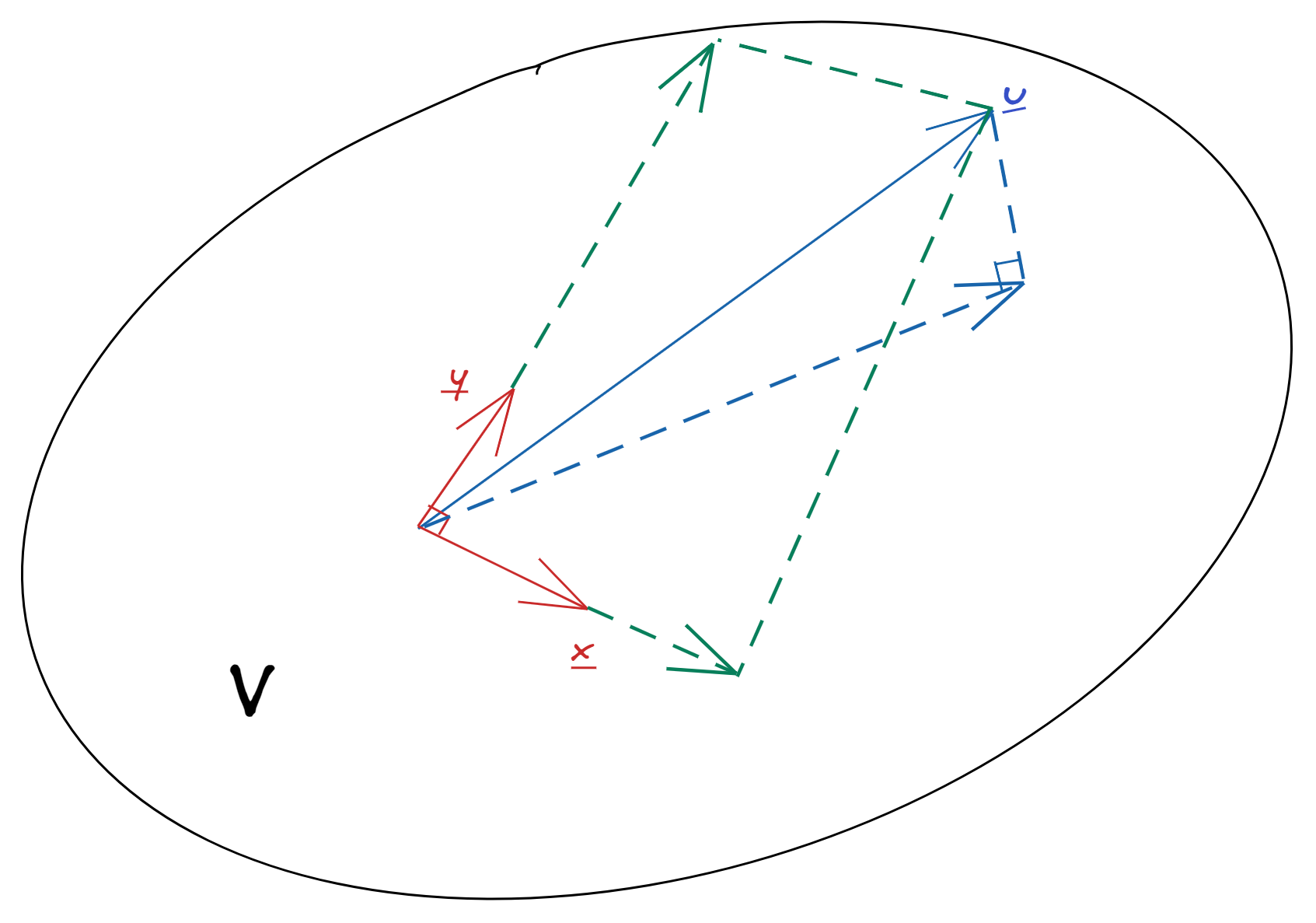
In the case of an orthonormal basis, this can be further simplified to $\sum_{i=1}^k (\boldsymbol{u}^\prime \boldsymbol{u}_i)\boldsymbol{u}_i$.
To prove this, let $\hat{\boldsymbol{u}} = P(\boldsymbol{u} \mid V)$2 and $\hat{\boldsymbol{u}}_i = P(\boldsymbol{u} \mid \boldsymbol{u}_i)$. The theorem says $\hat{\boldsymbol{u}} = \sum_{i=1}^k \hat{\boldsymbol{u}}_i$. We need to show $\sum_{i=1}^k \hat{\boldsymbol{u}}_i$ satisfies
- $\hat{\boldsymbol{u}} \in V$.
- For all $\boldsymbol{v} \in V$, $(\boldsymbol{u} - \hat{\boldsymbol{u}}) \cdot \boldsymbol{v} = 0$, or $(\boldsymbol{u} - \sum \hat{\boldsymbol{u}}_i ) \cdot \boldsymbol{v} = 0$.
First we write $\boldsymbol{v} = \sum \alpha_i \boldsymbol{u}_i$. Then,
$$ \begin{aligned} \left(\boldsymbol{u} - \sum_{i=1}^k \hat{\boldsymbol{u}}_i \right) \cdot \boldsymbol{v} &= \boldsymbol{u} \cdot \boldsymbol{v} - \sum_{i=1}^k \hat{\boldsymbol{u}}i \cdot \boldsymbol{v} \\ &= \boldsymbol{u} \cdot \left( \sum{i=1}^k \alpha_i \boldsymbol{u}i \right) - \sum{i=1}^k \left( \hat{\boldsymbol{u}}i \cdot \left( \sum{j=1}^k \alpha_j \boldsymbol{u}j \right) \right) \\ &= \sum{i=1}^k \alpha_i (\boldsymbol{u} \cdot \boldsymbol{u}i) - \sum{i=1}^k \sum_j \alpha_{j=1}^k (\underbrace{\hat{\boldsymbol{u}}i \cdot \boldsymbol{u}j}{\text{all zeros except } i=j}) \\ &= \sum{i=1}^k \alpha_i (\boldsymbol{u} \cdot \boldsymbol{u}i) - \sum{i=1}^k \alpha_i (\hat{\boldsymbol{u}}_i \cdot \boldsymbol{u}_i) \\ &= 0 \text{ because } \boldsymbol{u} \cdot \boldsymbol{u}_i = \hat{\boldsymbol{u}}_i \cdot \boldsymbol{u}_i \end{aligned} $$
Example
Let $V = \mathcal{L}(\boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3)$ where
$$ \begin{gathered} \boldsymbol{u}_1 = (1, 1, 1, 0, 0, 0)^\prime \\ \boldsymbol{u}_2 = (0, 0, 0, 1, 1, 0)^\prime \\ \boldsymbol{u}_3 = (0, 0, 0, 0, 0, 1)^\prime \end{gathered} $$
We have $\boldsymbol{u} = (6, 10, 5, 4, 8, 7)^\prime \in \mathbb{R}^6$ and want to find the projection of $\boldsymbol{u}$ onto $V$.
$$ \begin{aligned} P(\boldsymbol{u} \mid V) &= P(\boldsymbol{u} \mid \boldsymbol{u}_1) + P(\boldsymbol{u} \mid \boldsymbol{u}_2) + P(\boldsymbol{u} \mid \boldsymbol{u}_3) \\ &= \frac{6 + 10 + 5}{3}\boldsymbol{u}_1 + \frac{4 + 8}{2}\boldsymbol{u}_2 + \frac{7}{1}\boldsymbol{u}_3 \\ &= 7\boldsymbol{u}_1 + 6\boldsymbol{u}_2 + 7\boldsymbol{u}_3 \\ &= (7, 7, 7, 6, 6, 7)^\prime \end{aligned} $$
This is the vector in $V$ that’s the closest to $\boldsymbol{u}$.
If the given basis was orthonormal:
$$ \begin{gathered} \boldsymbol{z}_1 = (\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, 0, 0, 0)^\prime \\ \boldsymbol{z}_2 = (0, 0, 0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0)^\prime \\ \boldsymbol{z}_3 = (0, 0, 0, 0, 0, 1)^\prime \end{gathered} $$
The projection
$$ \begin{aligned} P(\boldsymbol{u} \mid V) &= (\boldsymbol{u} \cdot \boldsymbol{z}_1) \boldsymbol{z}_1 + (\boldsymbol{u} \cdot \boldsymbol{z}_2) \boldsymbol{z}_2 + (\boldsymbol{u} \cdot \boldsymbol{z}_3) \boldsymbol{z}_3 \\ &= \frac{6+10+5}{\sqrt{3}}\boldsymbol{z}_1 + \frac{4+8}{\sqrt{2}}\boldsymbol{z}_2 + 7\boldsymbol{z}_3 \\ &= (7, 7, 7, 6, 6, 7)^\prime \end{aligned} $$
| Sep 14 | Definitions in Arbitrary Linear Space | 6 min read |
| Aug 31 | Vector Space | 8 min read |
| Oct 12 | Matrix Inverse | 6 min read |
| Sep 30 | Linear Space of Matrices | 7 min read |
| Sep 28 | Orthogonalization | 5 min read |
 Yi's Knowledge Base
Yi's Knowledge Base